Thể tích khối trụ
Khối trụ là một hình dạng ba chiều được tạo thành bởi phép quay quanh trục cố định một mặt phẳng hình chữ nhật.
Đặc điểm
Hai mặt đáy là những mặt phẳng hình tròn song song với nhau.
Trục của hình trụ vuông góc với hai mặt đáy.
Mọi đường thẳng nằm trên một mặt phẳng đáy và vuông góc với trục đều là đường sinh của hình trụ.
Diện tích xung quanh bằng diện tích của một hình chữ nhật có chiều dài bằng chu vi đáy và chiều rộng bằng chiều cao của hình trụ.
Thể tích bằng thể tích của một hình hộp chữ nhật có chiều dài, chiều rộng và chiều cao lần lượt bằng đường kính đáy, chu vi đáy và chiều cao của hình trụ.
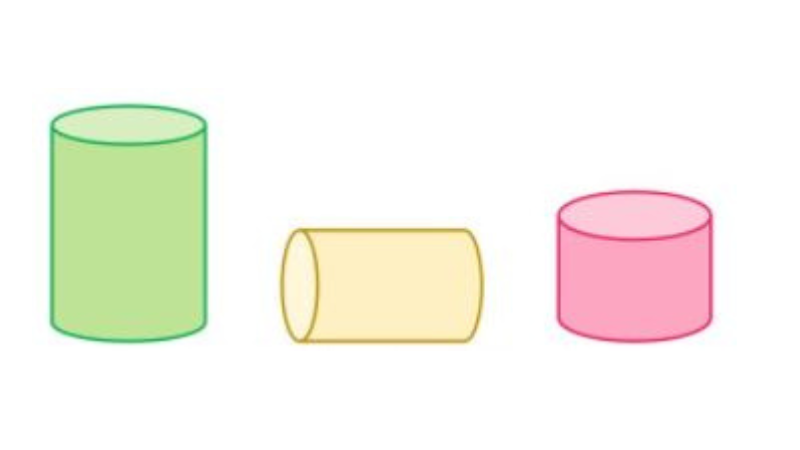
Khối trụTính chất về mặt hình học
Hai mặt đáy là hình tròn: Hai mặt đáy của khối trụ là những hình tròn đồng tâm, có bán kính bằng nhau và nằm trên hai mặt phẳng song song với nhau.
Trục của hình trụ vuông góc với hai mặt đáy: Đường thẳng đi qua tâm của hai mặt đáy và vuông góc với hai mặt phẳng chứa hai mặt đáy được gọi là trục của hình trụ.
Mọi đường thẳng nằm trên một mặt phẳng đáy và vuông góc với trục đều là đường sinh của hình trụ: Đường sinh của hình trụ là một đường thẳng đi qua một điểm trên một mặt phẳng đáy và vuông góc với trục của hình trụ.
Chiều cao của hình trụ bằng khoảng cách giữa hai mặt đáy: Chiều cao của hình trụ là khoảng cách giữa hai mặt phẳng chứa hai mặt đáy.
Diện tích xung quanh bằng diện tích của một hình chữ nhật có chiều dài bằng chu vi đáy và chiều rộng bằng chiều cao của hình trụ: Diện tích xung quanh của hình trụ là diện tích của phần mặt phẳng bao quanh hình trụ, được tính bằng công thức: Sxq = 2πrh, trong đó r là bán kính đáy và h là chiều cao của hình trụ.
Diện tích hai mặt đáy bằng diện tích của hai hình tròn có bán kính bằng bán kính đáy của hình trụ: Diện tích hai mặt đáy của hình trụ là diện tích của hai mặt phẳng chứa hai mặt đáy, được tính bằng công thức: Sđ = 2πr², trong đó r là bán kính đáy của hình trụ.
Diện tích toàn phần bằng tổng diện tích xung quanh và diện tích hai mặt đáy: Diện tích toàn phần của hình trụ là diện tích của toàn bộ bề mặt của hình trụ, được tính bằng công thức: Stp = Sxq + 2Sđ, trong đó Sxq là diện tích xung quanh, Sđ là diện tích hai mặt đáy.
Tham khảo: Thực đơn giảm cân trong 1 tuần
Tính chất về vị trí tương đối
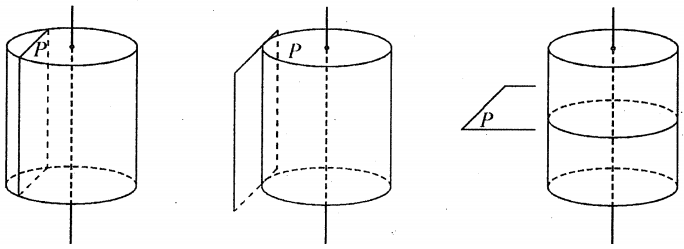
Vị trí tương đối giữa khối trụ và mặt phẳng:
- Tiếp xúc: Mặt phẳng tiếp xúc với khối trụ khi và chỉ khi nó có một điểm chung duy nhất với mặt phẳng chứa một mặt đáy của khối trụ.
- Cắt: Mặt phẳng cắt khối trụ khi và chỉ khi nó có nhiều hơn một điểm chung với mặt phẳng chứa một mặt đáy của khối trụ.
- Song song: Mặt phẳng song song với khối trụ khi và chỉ khi nó không có điểm chung nào với mặt phẳng chứa một mặt đáy của khối trụ.
Vị trí tương đối giữa hai khối trụ:
- Tiếp xúc: Hai khối trụ tiếp xúc khi và chỉ khi tâm của chúng cách nhau một khoảng bằng tổng bán kính của chúng.
- Cắt nhau: Hai khối trụ cắt nhau khi và chỉ khi tâm của chúng cách nhau một khoảng nhỏ hơn tổng bán kính của chúng nhưng lớn hơn hiệu số bán kính của chúng.
- Ngoài nhau: Hai khối trụ ngoài nhau khi và chỉ khi tâm của chúng cách nhau một khoảng lớn hơn tổng bán kính của chúng.
Khối trụDiện tích xung quanh (Sxq)
Công thức tính diện tích xung quanh của khối trụ là:
Sxq = 2πrh
Trong đó:
- Sxq: Diện tích xung quanh (đơn vị: mét vuông, cm vuông, ...)
- π: Số pi, xấp xỉ bằng 3,14159
- r: Bán kính đáy hình trụ (đơn vị: mét, cm, ...)
- h: Chiều cao hình trụ (đơn vị: mét, cm, ...)
Diện tích hai mặt đáy (Sđ)
Công thức tính diện tích hai mặt đáy của khối trụ là:
Sđ = 2πr²
Trong đó:
Sđ: Diện tích hai mặt đáy (đơn vị: mét vuông, cm vuông, ...)
- π: Số pi, xấp xỉ bằng 3,14159
- r: Bán kính đáy hình trụ (đơn vị: mét, cm, ...)
Diện tích toàn phần (Stp)
Công thức tính diện tích toàn phần của khối trụ là:
Stp = Sxq + 2Sđ
Trong đó:
- Stp: Diện tích toàn phần (đơn vị: mét vuông, cm vuông, ...)
- Sxq: Diện tích xung quanh (đơn vị: mét vuông, cm vuông, ...)
- Sđ: Diện tích hai mặt đáy (đơn vị: mét vuông, cm vuông, ...)
Ví dụ:
Một khối trụ có bán kính đáy là 5 cm và chiều cao là 10 cm. Diện tích xung quanh, diện tích hai mặt đáy và diện tích toàn phần của khối trụ này lần lượt là:
Sxq = 2π(5 cm)(10 cm) ≈ 314,16 cm²
Sđ = 2π(5 cm)² ≈ 78,54 cm²

Công thức khối trụThể tích khối trụ được tính bằng công thức
V = πr²h
Trong đó:
- V: Thể tích (đơn vị: mét khối, cm khối, ...)
- π: Số pi, xấp xỉ bằng 3,14159
- r: Bán kính đáy hình trụ (đơn vị: mét, cm, ...)
- h: Chiều cao hình trụ (đơn vị: mét, cm, ...)
Giải thích
- πr²: Diện tích mặt đáy của hình trụ.
- h: Chiều cao của hình trụ, là khoảng cách giữa hai mặt đáy.
- Thể tích của khối trụ bằng diện tích mặt đáy nhân với chiều cao.
Ví dụ
Một khối trụ có bán kính đáy là 5 cm và chiều cao là 10 cm. Thể tích của khối trụ này là:V = π(5 cm)²(10 cm) ≈ 785,39 cm³
Lưu ý
Các công thức trên chỉ áp dụng cho các khối trụ hoàn hảo, có bề mặt trơn nhẵn.
Khi tính thể tích khối trụ, cần đảm bảo đơn vị đo của bán kính và chiều cao phải nhất quán.
Ngoài ra
Diện tích xung quanh (Sxq) của khối trụ được tính bằng công thức:Sxq = 2πrh
Diện tích toàn phần (Stp) của khối trụ được tính bằng công thức:Stp = Sxq + 2Sđ
Trong đó
Sđ: Diện tích hai mặt đáy (đơn vị: mét vuông, cm vuông, ...)
Ví dụ:
Một khối trụ có bán kính đáy là 5 cm và chiều cao là 10 cm. Diện tích xung quanh, diện tích hai mặt đáy và diện tích toàn phần của khối trụ này lần lượt là:
Sxq = 2π(5 cm)(10 cm) ≈ 314,16 cm²
Sđ = 2π(5 cm)² ≈ 78,54 cm²
Stp = Sxq + 2Sđ ≈ 471,24 cm²
Trên đây là các thông tin về khối trụ cũng như các công thức về diện tích, thể tích khối trụ. Hi vọng các bạn đã có cho mình thông tin hữu ích.