Thể tích khối cầu
Khối cầu là một hình dạng ba chiều được tạo thành bởi tất cả các điểm cách đều một điểm cố định gọi là tâm (O) một khoảng bằng bán kính (r).
Đặc điểm
Bề mặt: Mọi điểm trên bề mặt khối cầu cách đều tâm O một khoảng bằng bán kính r.
Đường bao: Đường bao của khối cầu là một mặt cầu, là một mặt cong kín, không có cạnh, không có đỉnh.
Thể tích: Thể tích của khối cầu được tính theo công thức: V = 4/3 πr^3, trong đó π ≈ 3,14.
Diện tích: Diện tích mặt cầu được tính theo công thức: S = 4πr^2.
Khối cầu có nhiều ứng dụng trong thực tế, ví dụ như
Xây dựng: Khối cầu được sử dụng để xây dựng các công trình như mái vòm, bể chứa nước, v.v.
Kỹ thuật: Khối cầu được sử dụng trong các bộ phận máy móc như ổ trục, bánh răng, v.v.
Y học: Khối cầu được sử dụng trong các dụng cụ y tế như ống nghiệm, ống tiêm, v.v.
Thực phẩm: Khối cầu được sử dụng để tạo hình cho các loại thực phẩm như kẹo, bánh ngọt, v.v.
Khối cầu là một hình dạng ba chiều quan trọng với nhiều đặc điểm và ứng dụng trong thực tế.
Tham khảo: Các thì trong tiếng anh

Khối cầuTính chất về mặt hình học
Tâm và bán kính: Mọi điểm trên mặt cầu đều cách tâm (O) một khoảng bằng bán kính (r).
Đường bao: Đường bao của khối cầu là một mặt cầu, là một mặt cong kín, không có cạnh, không có đỉnh.
Góc tạo bởi hai tiếp tuyến: Góc tạo bởi hai tiếp tuyến tại một điểm bất kỳ trên mặt cầu bằng 90 độ.
Đường kính: Đường kính là đoạn thẳng đi qua tâm và nối hai điểm trên mặt cầu đối diện nhau. Độ dài đường kính bằng hai lần bán kính (D = 2r).
Tiếp tuyến: Qua một điểm bất kỳ trên mặt cầu chỉ có một tiếp tuyến duy nhất với mặt cầu tại điểm đó.
Góc tạo bởi tiếp tuyến và bán kính: Góc tạo bởi tiếp tuyến và bán kính tại điểm tiếp xúc bằng 90 độ.
Diện tích mặt cầu: Diện tích mặt cầu được tính theo công thức: S = 4πr^2, trong đó π ≈ 3,14.
Thể tích khối cầu: Thể tích khối cầu được tính theo công thức: V = 4/3 πr^3, trong đó π ≈ 3,14.
Tham khảo: Cách vẽ sơ đồ tư duy đẹp
Tính chất về vị trí tương đối
Vị trí tương đối giữa khối cầu và mặt phẳng:
- Tiếp xúc: Mặt phẳng tiếp xúc với khối cầu khi và chỉ khi nó có một điểm chung duy nhất với mặt cầu.
- Cắt: Mặt phẳng cắt khối cầu khi và chỉ khi nó có nhiều hơn một điểm chung với mặt cầu.
- Song song: Mặt phẳng song song với khối cầu khi và chỉ khi nó không có điểm chung nào với mặt cầu.
Vị trí tương đối giữa hai khối cầu:
- Tiếp xúc: Hai khối cầu tiếp xúc khi và chỉ khi tâm của chúng cách nhau một khoảng bằng tổng bán kính của chúng.
- Cắt nhau: Hai khối cầu cắt nhau khi và chỉ khi tâm của chúng cách nhau một khoảng nhỏ hơn tổng bán kính của chúng nhưng lớn hơn hiệu số bán kính của chúng.
- Ngoài nhau: Hai khối cầu ngoài nhau khi và chỉ khi tâm của chúng cách nhau một khoảng lớn hơn tổng bán kính của chúng.
Một số tính chất khác
Khối cầu là hình có trục đối xứng: Mọi đường thẳng qua tâm của khối cầu đều là trục đối xứng của nó.
Khối cầu là hình có tâm đối xứng: Mọi mặt phẳng qua tâm của khối cầu đều là mặt phẳng đối xứng của nó.
Khối cầu là hình có mặt phẳng đối xứng: Mọi mặt phẳng tiếp xúc với khối cầu đều là mặt phẳng đối xứng của nó.
Khối cầu
Diện tích mặt cầu
Diện tích mặt cầu được tính bằng công thức:
S = 4πr²
Trong đó:
S: Diện tích mặt cầu (đơn vị mét vuông, cm vuông, ...)
π: Số pi, xấp xỉ bằng 3,14159
r: Bán kính mặt cầu (đơn vị mét, cm, ...)
Ví dụ:
Một quả bóng đá có bán kính 10 cm. Diện tích mặt cầu của quả bóng đá này là: S = 4π(10 cm)² ≈ 1256,64 cm²
Thể tích khối cầu
Thể tích hình cầu được tính bằng công thức:
V = 4/3πr³
Trong đó:
V: Thể tích hình cầu (đơn vị mét khối, cm khối, ...)
π: Số pi, xấp xỉ bằng 3,14159
r: Bán kính hình cầu (đơn vị mét, cm, ...)
Ví dụ:
Một quả cầu thủy tinh có bán kính 5 cm. Thể tích của quả cầu thủy tinh này là: V = 4/3π(5 cm)³ ≈ 523,6 cm³
Ngoài ra, bạn cũng có thể sử dụng các công thức sau để tính diện tích mặt cầu và thể tích hình cầu theo đường kính (D):
Diện tích mặt cầu
S = πD²
Thể tích hình cầu
V = (4/3)πD³/6
Ví dụ:
Một quả bóng rổ có đường kính 24 cm. Diện tích mặt cầu của quả bóng rổ này là: S = π(24 cm)² ≈ 1796 cm² Thể tích của quả bóng rổ này là: V = (4/3)π(24 cm)³/6 ≈ 4188 cm³
Tham khảo: Bảng tuần hoàn hóa học tiếng Anh
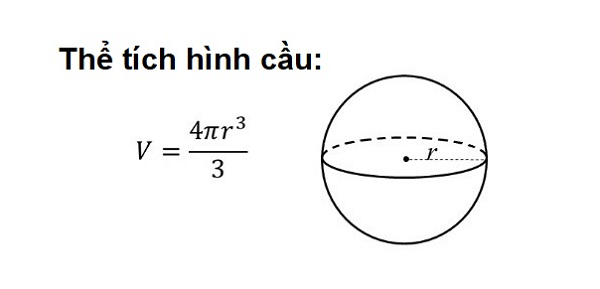
Thể tích hình cầuThể tích hình cầu tỉ lệ lập phương với bán kính của nó.
Công thức tính thể tích hình cầu là:
V = (4/3)πR^3
Trong đó:
V: Thể tích hình cầu (đơn vị mét khối, cm khối, ...)
π: Số pi, xấp xỉ bằng 3,14159
R: Bán kính hình cầu (đơn vị mét, cm, ...)
Điều này có nghĩa là:
Nếu ta tăng gấp đôi bán kính của hình cầu, thì thể tích của nó sẽ tăng gấp tám lần.
Nếu ta giảm một nửa bán kính của hình cầu, thì thể tích của nó sẽ giảm đi bốn lần.
Ví dụ:
Giả sử một quả cầu có bán kính là 2 cm. Thể tích của quả cầu này là: V = (4/3)π(2 cm)^3 ≈ 33,51 cm^3
Nếu ta tăng bán kính của quả cầu này lên gấp đôi (tức là 4 cm), thì thể tích của nó sẽ tăng lên thành: V = (4/3)π(4 cm)^3 ≈ 268,08 cm^3
Như vậy, thể tích của quả cầu đã tăng gấp 8 lần so với ban đầu.
Trên đây là một số thông tin về khối cầu cũng như các công thức về diện tích, thể tích khối cầu. Hi vọng các bạn sẽ có cho mình thông tin hữu ích.
>> Tham khảo: Múi giờ Nhật Bản và Việt Nam