Thể tích khối cầu
Hình cầu
Định nghĩa: Hình cầu là một hình học không gian được tạo thành bởi tất cả các điểm cách một điểm cố định (gọi là tâm O) một khoảng bằng bán kính (R). Nói cách khác, hình cầu là tập hợp các điểm M trong không gian thỏa mãn điều kiện:
OM ≤ R
Với O là tâm cầu và R là bán kính cầu.
Đặc điểm:
Bề mặt: Bề mặt của hình cầu là một mặt cong gọi là mặt cầu. Mặt cầu không có mép, không có đỉnh và có diện tích hữu hạn.
Đường kính: Đường kính của hình cầu là đoạn thẳng đi qua tâm và nối hai điểm trên mặt cầu bất kỳ. Độ dài đường kính bằng hai lần bán kính, ký hiệu là D = 2R.
Thể tích: Thể tích của hình cầu là thể tích của khối được giới hạn bởi mặt cầu. Thể tích hình cầu được tính bằng công thức:V = (4/3)πR³ Với π là số pi xấp xỉ bằng 3,14159.
Khối cầu
Định nghĩa: Khối cầu là một khối được tạo thành bởi hình cầu và tất cả các điểm nằm bên trong hình cầu đó. Nói cách khác, khối cầu là tập hợp các điểm M trong không gian thỏa mãn điều kiện:
OM ≤ R
Với O là tâm cầu và R là bán kính cầu.
Đặc điểm:
Khối cầu có tất cả các đặc điểm của hình cầu, bao gồm: bề mặt cong, đường kính, thể tích.
Ngoài ra, khối cầu còn có thể tích riêng, được tính bằng công thức:V = (4/3)πR³ Với π là số pi xấp xỉ bằng 3,14159.
Phân biệt hình cầu và khối cầu
Hình cầu chỉ là bề mặt cong bao quanh khối cầu, không bao gồm các điểm bên trong.
Khối cầu bao gồm hình cầu và tất cả các điểm nằm bên trong hình cầu đó.
Hình cầu không có thể tích, chỉ có diện tích.
Khối cầu có thể tích được tính bằng công thức: V = (4/3)πR³.
Ví dụ
Hình cầu: Quả bóng đá, quả địa cầu (chỉ là bề mặt bên ngoài).
Khối cầu: Quả bóng rổ, quả cam (bao gồm cả vỏ và phần ruột bên trong).
Hình cầu và khối cầu là hai khái niệm liên quan mật thiết trong hình học không gian. Hình cầu là bề mặt cong bao quanh khối cầu, và khối cầu bao gồm cả hình cầu và các điểm nằm bên trong hình cầu đó. Khối cầu có thể tích được tính bằng công thức, trong khi hình cầu không có thể tích.
Tham khảo: Phụ nữ uống đông trùng hạ thảo có tốt không?
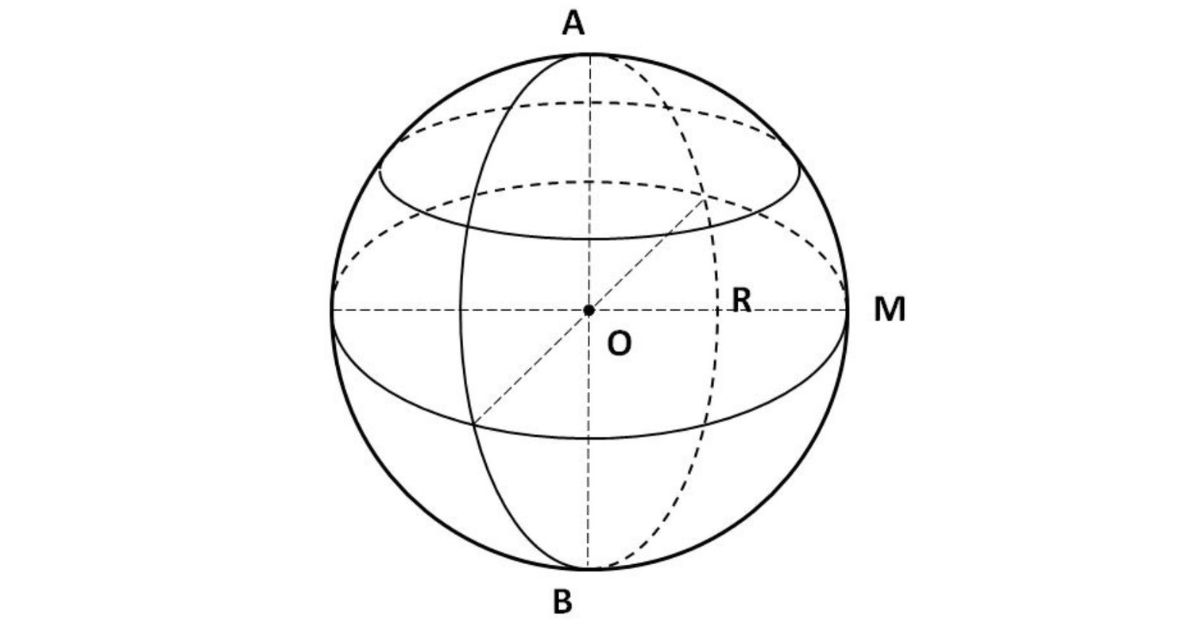
Khối cầu, hình cầuDiện tích mặt cầu
Diện tích mặt cầu (S) được tính bằng công thức:
S = 4πR²
Với:
S: Diện tích mặt cầu (đơn vị cm², m², inch²,...).
π: Số pi, xấp xỉ bằng 3,14159.
R: Bán kính của hình cầu (đơn vị cm, m, inch,...).
Thể tích khối cầu
Thể tích (V) của khối cầu được tính bằng công thức:
V = (4/3)πR³
Với:
V: Thể tích (đơn vị cm³, m³, lít, gallon,...).
π: Số pi, xấp xỉ bằng 3,14159.
R: Bán kính của hình cầu (đơn vị cm, m, inch,...).
Lưu ý
Các công thức trên chỉ áp dụng cho trường hợp hình cầu hoàn hảo, không bị méo mó hay khuyết tật.
Đơn vị đo diện tích thường là cm², m², inch²,...
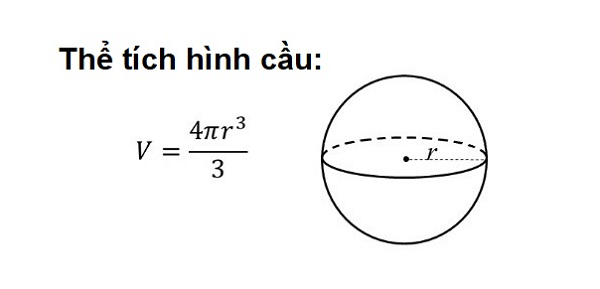
Công thức diện tích, thể tích của khối cầuPhân tích đề bài
Xác định các yếu tố được cho trong đề bài, bao gồm bán kính (R) hoặc đường kính (D) của hình cầu.
Chuyển đổi đơn vị đo nếu cần thiết (ví dụ: từ cm sang m).
Chọn công thức tính thể tích
Sử dụng công thức tính thể tích của khối cầu: V = (4/3)πR³ Với R là bán kính của hình cầu (đơn vị cm, m, inch,...).
Nếu đề bài cho đường kính (D), bạn có thể tính bán kính (R) bằng công thức:R = D/2
Thay số và tính toán
Thay giá trị bán kính (R) đã biết vào công thức tính thể tích.
Sử dụng máy tính để tính toán kết quả.
Kiểm tra kết quả
Xác định xem kết quả có hợp lý hay không dựa trên các yếu tố trong đề bài và đơn vị đo đã sử dụng.
Tham khảo: Công thức hạ bậc

Khối cầu, hình cầuBài tập 1
Cho một hình cầu có bán kính R = 4 cm.
a) Tính diện tích mặt cầu. b) Tính thể tích của khối cầu.
Bài tập 2
Một quả bóng rổ có đường kính 24 cm.
a) Tính bán kính của quả bóng rổ. b) Tính diện tích mặt cầu của quả bóng rổ. c) Tính thể tích của khối cầu của quả bóng rổ.
Bài tập 3
Một bể nước hình cầu có thể tích 113,04 m³. Tính bán kính của bể nước.
Bài tập 4
Một quả cầu đá có diện tích mặt cầu là 125,66 cm². Tính bán kính và thể tích của quả cầu đá.
Bài tập 5
Một cái bình thủy tinh hình cầu có bán kính x cm. Biết thể tích của bình là 33,51 cm³. Tính giá trị của x.
Bài giải
Bài tập 1
a) Diện tích mặt cầu: S = 4πR² = 4π(4 cm)² = 64π cm²
b) Thể tích khối cầu: V = (4/3)πR³ = (4/3)π(4 cm)³ = 256π cm³
Bài tập 2
a) Bán kính của quả bóng rổ: R = D/2 = 24 cm/2 = 12 cm
b) Diện tích mặt cầu của quả bóng rổ: S = 4πR² = 4π(12 cm)² = 576π cm²
c) Thể tích khối cầu của quả bóng rổ: V = (4/3)πR³ = (4/3)π(12 cm)³ = 904,78 cm³
Bài tập 3
Thể tích của bể nước: V = (4/3)πR³ = 113,04 m³
Bán kính của bể nước: R = ³√(3V / 4π) = ³√(3 * 113,04 m³ / 4π) ≈ 2,5 m
Bài tập 4
Bán kính của quả cầu đá: R = √(S / 4π) = √(125,66 cm² / 4π) ≈ 5 cm
Thể tích của quả cầu đá: V = (4/3)πR³ = (4/3)π(5 cm)³ ≈ 523,6 cm³
Bài tập 5
Thể tích của bình thủy tinh: V = 33,51 cm³
Bán kính của bình thủy tinh: R = ³√(3V / 4π) = ³√(3 * 33,51 cm³ / 4π) ≈ 3 cm
Vậy giá trị của x là 3.
Trên đây là một số thông tin về khối cầu và công thức tính diện tích, thể tích khối cầu. Hi vọng các bạn đã có cho mình thông tin hữu ích.