Thể tích khối trụ
Hình trụ là một hình học không gian được sinh ra bởi một mặt phẳng quay quanh một trục cố định. Hình trụ có hai mặt phẳng tròn song song gọi là đáy, được nối với nhau bởi một mặt cong gọi là mặt trụ.
Đặc điểm
Chiều cao (h) là khoảng cách giữa hai đáy.
Bán kính (r) là khoảng cách từ tâm một đáy đến một điểm bất kỳ trên đường tròn đáy.
Hai mặt phẳng đáy có diện tích bằng nhau và đường tròn đáy này ngoại tiếp một hình vuông có cạnh bằng chiều cao (h) của hình trụ.
Hình dung
Hãy tưởng tượng bạn lấy một tờ giấy hình chữ nhật và cuộn tròn nó quanh một cây bút chì. Khi đó, tờ giấy sẽ tạo thành một hình trụ. Mặt phẳng của tờ giấy sẽ trở thành mặt xung quanh của hình trụ, hai đầu của tờ giấy sẽ trở thành hai mặt đáy hình tròn, và trục của cây bút chì sẽ trở thành trục của hình trụ.
Hình trụ trong thực tế
Hình trụ được ứng dụng rộng rãi trong đời sống, ví dụ như:
Cột trụ nhà: Hình trụ được sử dụng để làm cột trụ cho nhà cửa, giúp đỡ trọng lượng của các tầng trên.
Ống nước: Ống nước thường có dạng hình trụ, giúp vận chuyển nước từ nơi này đến nơi khác.
Hộp đựng thức ăn: Hộp đựng thức ăn, lon bia, lon nước ngọt,... thường có dạng hình trụ.
Lò xo: Lò xo được cấu tạo từ nhiều vòng xoắn lại với nhau, tạo thành hình trụ.
Phân biệt hình trụ và hình nón
Hình trụ và hình nón là hai hình học không gian có nhiều điểm tương đồng, nhưng cũng có một số điểm khác biệt chính:
Hình trụ:
Hai mặt đáy song song và bằng nhau.
Mặt xung quanh là mặt cong.
Trục vuông góc với hai mặt đáy.
Hình nón:
Hai mặt đáy không song song và bằng nhau.
Mặt xung quanh là mặt cong.
Trục đi qua đỉnh và tâm đáy.
Hình trụ là một hình học không gian quan trọng với nhiều ứng dụng trong thực tế. Hiểu rõ về hình trụ sẽ giúp bạn giải quyết các bài toán liên quan một cách dễ dàng và chính xác hơn.
Tham khảo: Phụ nữ uống đông trùng hạ thảo có tốt không?
Hình trụHình trụ là một hình học không gian được sinh ra bởi một mặt phẳng quay quanh một trục cố định. Hình trụ có hai mặt phẳng tròn song song gọi là đáy, được nối với nhau bởi một mặt cong gọi là mặt trụ.
Công thức tính diện tích
Diện tích xung quanh (Sxq):
Sxq = 2πrh
Với:
Sxq: Diện tích xung quanh (đơn vị cm², m²,...).
π: Số pi, xấp xỉ bằng 3,14159.
r: Bán kính đáy (đơn vị cm, m, inch,...).
h: Chiều cao (đơn vị cm, m, inch,...).
Diện tích toàn phần (Stp):
Stp = Sxq + 2Sday
Với:
Stp: Diện tích toàn phần (đơn vị cm², m²,...).
Sxq: Diện tích xung quanh (đơn vị cm², m²,...).
Sday: Diện tích một đáy (đơn vị cm², m²,...).
Sday = πr²
Công thức tính thể tích
Thể tích (V):
V = Sday.h
Với:
V: Thể tích (đơn vị cm³, m³, lít, gallon,...).
Sday: Diện tích một đáy (đơn vị cm², m²,...).
Sday = πr²
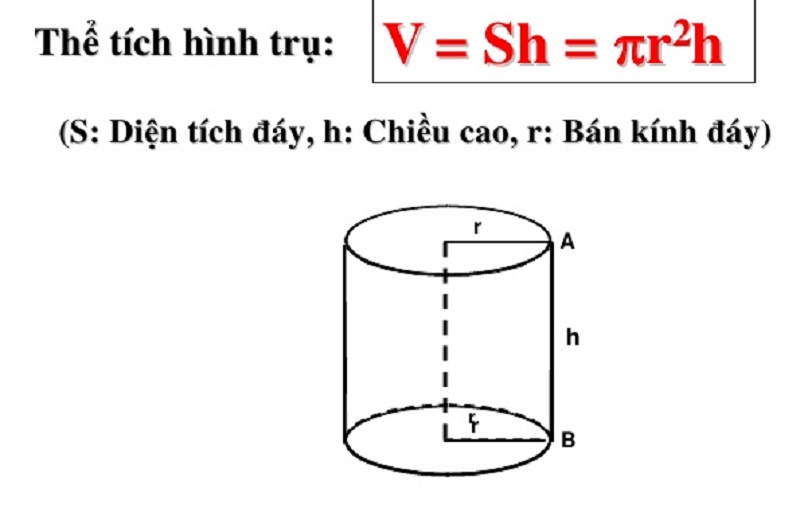
Công thức thể tích hình trụ, hình nónPhân tích đề bài
Xác định các yếu tố được cho trong đề bài, bao gồm bán kính (R) hoặc đường kính (D) và chiều cao (H) của hình trụ.
Chuyển đổi đơn vị đo nếu cần thiết (ví dụ: từ cm sang m).
Chọn công thức tính diện tích và thể tích
Thay số và tính toán
Thay giá trị bán kính (R) hoặc đường kính (D) và chiều cao (H) đã biết vào công thức tính diện tích và thể tích.
Sử dụng máy tính để tính toán kết quả.
Kiểm tra kết quả
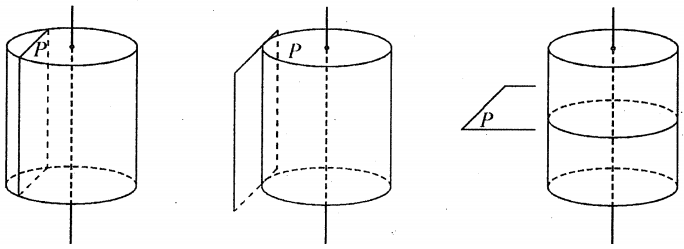
Hình trụ, khối trụBài tập 1
Cho một hình trụ có bán kính đáy R = 3 cm và chiều cao H = 5 cm.
a) Tính diện tích xung quanh của hình trụ. b) Tính diện tích toàn phần của hình trụ. c) Tính thể tích của hình trụ.
Bài tập 2
Một khối gỗ hình trụ có bán kính đáy R = 4 cm và chiều cao H = 8 cm. Người ta khoét bỏ một khối gỗ hình trụ nhỏ hơn đồng trục với khối trụ lớn sao cho chiều cao của khối gỗ nhỏ bằng 2/3 chiều cao của khối gỗ lớn và bán kính đáy của khối gỗ nhỏ bằng 1/2 bán kính đáy của khối gỗ lớn. Tính thể tích gỗ còn lại.
Bài tập 3
Một bể nước hình trụ có thể tích V = 113,04 m³. Tính bán kính đáy của bể nước.
Bài tập 4
Một quả cầu đá có diện tích mặt cầu S = 125,66 cm². Tính bán kính và thể tích của quả cầu đá.
Bài tập 5
Một cái bình thủy tinh hình trụ có bán kính đáy R là x cm. Biết thể tích của bình là 33,51 cm³. Tính giá trị của x.
Tham khảo: Phân tích đất nước lớp 12
Hướng dẫn giải
Bài tập 1
a) Diện tích xung quanh: * Sxq = 2πRH = 2π(3 cm)(5 cm) ≈ 94,25 cm²
b) Diện tích một đáy: * Sday = πR² = π(3 cm)² ≈ 28,27 cm²
c) Diện tích toàn phần: * Stp = Sxq + 2Sday ≈ 94,25 cm² + 2(28,27 cm²) ≈ 150,79 cm²
Thể tích: * V = Sday.H ≈ 28,27 cm² (5 cm) ≈ 141,35 cm³
Bài tập 2
Bán kính đáy khối gỗ nhỏ: * R_nhỏ = R/2 = 4 cm/2 = 2 cm
Chiều cao khối gỗ nhỏ: * H_nhỏ = 2/3 H = 2/3 (8 cm) = 16/3 cm
Thể tích khối gỗ nhỏ: * V_nhỏ = πR_nhỏ²H_nhỏ = π(2 cm)²(16/3 cm) ≈ 32/3π cm³
Thể tích khối gỗ lớn: * V_lớn = πR²H = π(4 cm)²(8 cm) ≈ 128π cm³
Thể tích gỗ còn lại: * V_còn lại = V_lớn - V_nhỏ ≈ 128π cm³ - 32/3π cm³ ≈ 118,22π cm³
Bài tập 3
Thể tích của bể nước: * V = πR²H = 113,04 m³
Bán kính đáy của bể nước: * R = √(V / πH) ≈ √(113,04 m³ / π(8 m)) ≈ 2,5 m
Bài tập 4
Bán kính của quả cầu đá: * R = √(S / 4π) = √(125,66 cm² / 4π) ≈ 5 cm
Thể tích của quả cầu đá: * V = (4/3)πR³ = (4/3)π(5 cm)³ ≈ 523,6 cm³
Bài tập 5
Thể tích của bình thủy tinh: * V = 33,51 cm³
Bán kính đáy của bình thủy tinh: * R = √(V / πH) = √(33,51 cm³ / π(x cm)) ≈ √(33,51 / πx) cm
Trên đây là các thông tin về khối trụ và thể tích khối trụ. Hi vọng các bạn đã có thông tin hữu ích.