Thể tích khối cầu

1. Khối cầu là gì?

Khối cầu là một hình học không gian ba chiều, trong đó tất cả các điểm trên bề mặt đều cách đều một điểm cố định được gọi là tâm. Khoảng cách từ mọi điểm trên bề mặt khối cầu đến tâm được gọi là bán kính.

Đặc điểm của khối cầu

Tâm: Điểm nằm ở giữa khối cầu.

Bán kính (R): Khoảng cách từ tâm đến bất kỳ điểm nào trên bề mặt khối cầu.

Đường kính (D): Đường thẳng đi qua tâm và có hai điểm nằm trên bề mặt khối cầu, bằng hai lần bán kính (D = 2R).

Bề mặt khối cầu: Tổng hợp tất cả các điểm cách tâm một khoảng bằng bán kính.

Tóm lại, khối cầu là một hình học không gian ba chiều đặc biệt với nhiều ứng dụng thực tế và được đặc trưng bởi bán kính, diện tích bề mặt và thể tích.

Học sinh trong giờ toán

2. Công thức tính thể tích khối cầu

Khối cầu là một hình học ba chiều mà tất cả các điểm trên bề mặt đều cách đều một điểm gọi là tâm. Thể tích của khối cầu, đại diện cho không gian mà nó chiếm, có thể được tính bằng công thức sau:

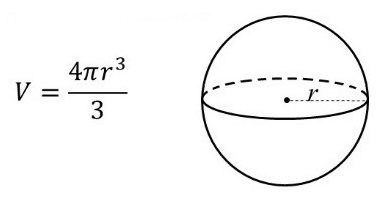
Công thức tính thể tích khối cầu

Trong đó:

V là thể tích của khối cầu.

R là bán kính của khối cầu.

π là hằng số Pi, xấp xỉ bằng 3.14159.
Tham khảo: Các thì trong tiếng anh

3. Làm thế nào để tìm thể tích khối cầu?

Làm thế nào để tìm thể tích của khối cầu?

Để tính thể tích của khối cầu, bạn cần biết bán kính của khối cầu và áp dụng công thức toán học liên quan. Dưới đây là các bước cụ thể để tính thể tích của khối cầu.

Bước 1: Xác định bán kính của khối cầu

Bán kính 𝑅 là khoảng cách từ tâm của khối cầu đến bất kỳ điểm nào trên bề mặt của nó. Bạn có thể đo trực tiếp bán kính hoặc lấy từ các thông tin có sẵn.

Bước 2: Sử dụng công thức tính thể tích

Thể tích của khối cầu được tính bằng công thức:

Bước 3: Thay giá trị bán kính vào công thức

Bạn thay giá trị của bán kính 𝑅 vào công thức trên và tính toán để tìm thể tích.

Để tìm thể tích của khối cầu, bạn chỉ cần biết bán kính của nó và sử dụng công thức 

𝑉= πR 3

 . Việc thay giá trị bán kính vào công thức và thực hiện các phép tính sẽ giúp bạn xác định thể tích của khối cầu một cách chính xác.

Công thức được ứng dụng vào nhiều ngành

4. Ứng dụng thể tích khối cầu 

Thể tích khối cầu có ứng dụng rộng rãi trong nhiều lĩnh vực đời sống:

Công nghiệp thực phẩm: Khi chế biến thực phẩm dạng hình cầu như kem viên hay bánh tròn, việc tính toán thể tích giúp xác định lượng nguyên liệu cần thiết và kiểm soát kích thước sản phẩm.

Thiết kế thể thao: Trong các môn thể thao như bóng rổ hay bóng đá, thể tích của quả bóng ảnh hưởng đến thiết kế và hiệu suất của sản phẩm.

Hàng không vũ trụ: Trong thiết kế và chế tạo các thiết bị như vệ tinh hoặc các mô-đun không gian có dạng hình cầu, việc tính toán thể tích giúp tối ưu hóa không gian và trọng lượng.

Dược phẩm: Các viên thuốc có hình dạng viên cầu có thể yêu cầu tính toán thể tích để đảm bảo đúng liều lượng thuốc trong mỗi viên.

Kỹ thuật xây dựng: Trong một số ứng dụng xây dựng, như việc thiết kế bể chứa hình cầu hay các cấu trúc dạng hình cầu, việc tính toán thể tích giúp xác định kích thước và khả năng chứa đựng.