Thể tích khối trụ
Khối trụ là một hình học không gian ba chiều, với hai đáy là hai hình tròn bằng nhau và song song, được kết nối bởi một mặt cong. Để tính thể tích của khối trụ, bạn cần biết bán kính của đáy và chiều cao của khối trụ.
Thể tích của khối trụ được tính bằng công thức:
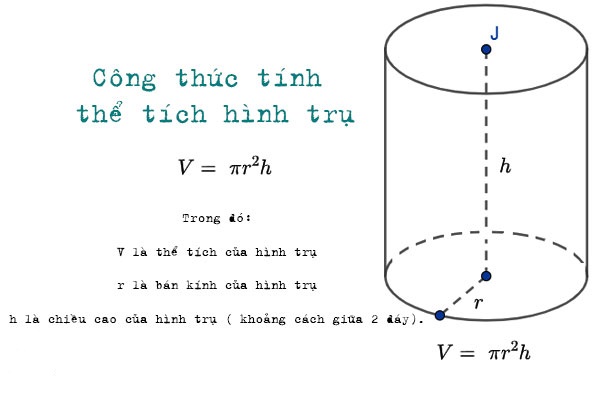Công thức tính thể tích của khối trụTrong đó:
V là thể tích của khối trụ.
R là bán kính của đáy khối trụ.
H là chiều cao của khối trụ.
π là hằng số Pi, xấp xỉ bằng 3.14159.
Bước 1: Xác định bán kính và chiều cao của khối trụ
Bán kính (R) Khoảng cách từ tâm của đáy hình tròn đến bất kỳ điểm nào trên đường tròn đó.
Chiều cao 𝐻 Khoảng cách thẳng đứng giữa hai đáy hình tròn của khối trụ.
Bước 2: Sử dụng công thức tính thể tích
Sau khi xác định bán kính và chiều cao, bạn thay các giá trị này vào công thức để tính thể tích.
Việc thay giá trị của bán kính và chiều cao vào công thức và thực hiện các phép tính sẽ giúp bạn xác định thể tích của khối trụ một cách chính xác.
Để giải các bài tập tính thể tích của khối trụ mà không cần viết lại công thức, bạn có thể làm theo các bước sau:
Bước 1: Hiểu rõ bài toán
Đọc kỹ đề bài để xác định các thông số quan trọng như:
Bán kính của đáy khối trụ 𝑅
Chiều cao của khối trụ 𝐻
Bước 2: Xác định các giá trị cần thiết
Tìm ra giá trị của bán kính và chiều cao từ đề bài. Đảm bảo rằng các giá trị này có đơn vị đo lường thống nhất (ví dụ: cả hai đều tính bằng cm hoặc m).
Bước 3: Tính diện tích đáy của khối trụ
Diện tích của đáy hình tròn được tính bằng cách nhân giá trị bán kính với chính nó và với hằng số Pi (π). Ví dụ:
Nếu bán kính là 3 cm, diện tích đáy sẽ là diện tích của hình tròn có bán kính 3 cm.
Bước 4: Tính thể tích của khối trụ
Nhân diện tích đáy với chiều cao của khối trụ để có thể tích. Thể tích sẽ bằng diện tích đáy nhân với chiều cao.
Tham khảo: Diện tích tam giác vuông
Khối trụVí dụ minh họa
Ví dụ 1: Tính thể tích của khối trụ có bán kính 4 cm và chiều cao 10 cm.
Xác định giá trị bán kính và chiều cao:
Bán kính: 4 cm.
Chiều cao: 10 cm.
Tính diện tích đáy:
Diện tích đáy của hình tròn có bán kính 4 cm.
Tính thể tích:
Nhân diện tích đáy vừa tính với chiều cao 10 cm.
Ví dụ 2: Tính thể tích của khối trụ có bán kính 2 m và chiều cao 5 m.
Xác định giá trị bán kính và chiều cao:
Bán kính: 2 m.
Chiều cao: 5 m.
Tính diện tích đáy:
Diện tích đáy của hình tròn có bán kính 2 m.
Tính thể tích:
Nhân diện tích đáy vừa tính với chiều cao 5 m.
Lưu ý
Hãy chắc chắn rằng các giá trị sử dụng trong phép tính có đơn vị đo lường thống nhất.
Hằng số Pi (π) có thể được sử dụng với giá trị gần đúng là 3.14159 hoặc với nhiều chữ số thập phân hơn để tăng độ chính xác.
Đơn vị của thể tích sẽ là đơn vị khối của bán kính và chiều cao. Ví dụ, nếu bán kính và chiều cao tính bằng cm thì thể tích sẽ tính bằng cm³, nếu bán kính và chiều cao tính bằng m thì thể tích sẽ tính bằng m³.
Tóm lại
Để giải các bài tập tính thể tích của khối trụ:
Xác định giá trị bán kính và chiều cao từ đề bài.
Tính diện tích đáy của khối trụ bằng cách nhân giá trị bán kính với chính nó và với Pi.
Nhân diện tích đáy với chiều cao của khối trụ để có thể tích.
Tham khảo: Bảng chữ cái hiragana
Ứng dụng nhiều trong lĩnh vực xây dựngThể tích khối trụ có nhiều ứng dụng thực tế trong đời sống và các lĩnh vực kỹ thuật. Dưới đây là một số ví dụ điển hình về cách thể tích của khối trụ được sử dụng:
Xây dựng và kiến trúc
Bể chứa nước: Các bể chứa nước thường có dạng khối trụ để tối ưu hóa không gian và đảm bảo áp lực nước đồng đều.
Cột trụ trong xây dựng: Các cột trụ trong các công trình xây dựng thường có dạng hình trụ để chịu lực tốt hơn và tiết kiệm vật liệu.
Công nghiệp và sản xuất
Bình chứa và thùng phuy: Trong các ngành công nghiệp, các bình chứa hóa chất, dầu, và các chất lỏng khác thường có dạng khối trụ để dễ dàng trong việc lưu trữ và vận chuyển.
Xi lanh thủy lực và khí nén: Các thiết bị này sử dụng khối trụ để tạo ra lực nén và lực đẩy trong các hệ thống máy móc.
Y tế và dược phẩm
Ống tiêm: Các ống tiêm và thiết bị chứa thuốc thường có dạng khối trụ để đảm bảo liều lượng chính xác và dễ sử dụng.
Viên thuốc con nhộng: Một số loại viên thuốc được sản xuất dưới dạng khối trụ để dễ dàng nuốt và bảo quản.
Tham khảo: Quảng cáo google adwords trọn gói
Giao thông vận tải
Bồn chứa nhiên liệu: Các xe tải chở xăng dầu thường có bồn chứa dạng khối trụ để đảm bảo an toàn và tối ưu hóa không gian chứa.
Đường hầm: Một số đường hầm có dạng khối trụ để đảm bảo cấu trúc ổn định và khả năng chịu lực tốt.
Nghiên cứu và giáo dục
Thí nghiệm khoa học: Trong các phòng thí nghiệm, nhiều thiết bị đo lường và chứa mẫu vật có dạng khối trụ để đảm bảo độ chính xác và dễ sử dụng.
Giảng dạy: Các mô hình khối trụ thường được sử dụng trong giảng dạy toán học và vật lý để minh họa các khái niệm liên quan đến thể tích và hình học không gian.
Đời sống hàng ngày
Ống nước và ống thoát nước: Các hệ thống ống nước và thoát nước trong nhà thường có dạng khối trụ để đảm bảo dòng chảy liên tục và hiệu quả.
Lon nước giải khát: Các lon nước giải khát và thực phẩm đóng hộp thường có dạng khối trụ để dễ dàng sản xuất, vận chuyển và lưu trữ.
Thể tích khối trụ có nhiều ứng dụng quan trọng trong đời sống, từ xây dựng, công nghiệp, y tế đến giao thông vận tải và giáo dục. Khối trụ được ưa chuộng trong nhiều lĩnh vực nhờ khả năng tối ưu hóa không gian, đảm bảo an toàn và chịu lực tốt.